Probabilitas dan Statistik : Distribusi Normal [PAPER]

  

BAB I

PENDAHULUAN

1.1 Latar Belakang

Dalam kehidupan sehari-hari kita sering dihadapkan dengan beberapa pilihan dan harus memilih dari beberapa pilihan tersebut. Biasanya dihadapkan dengan kemungkinan-kemungkinan suatu kejadian yang mungkin terjadi dan harus pintar-pintar mengambil sikap jika menemukan keadaan seperti ini, misalkan saja pada saat ingin bepergian, saat melihat langit, terlihat mendung. Dalam keadaaan ini maka dihadapkan antara 2 permasalahan, yaitu kemungkinan terjadinya hujan serta kemungkinan langit hanya mendung saja dan tidak akan turunnya hujan. Statistik yang membantu permasalahan dalam hal ini adalah probabilitas.

Statistika diambil dari kata statistics, yaitu suatu ilmu yang mempelajari bagaimana cara merencanakan, mengumpulkan, menganalisis, mengintepretasi, dan mempresentasikan data. Pada umumnya statistika adalah ilmu yang berhubungan dengan sekumpulan data yang biasanya dapat diolah dengan ilmu probabilitas. [8]

Probabilitas adalah suatu ilmu untuk memprediksi suatu kejadian atau dapat disebut peluang suatu kejadian berdasarkan pendekatan secara matematis. Sekedar informasi tambahan, ilmu peluang atau probabilitas ditemukan oleh pakar judi pada jaman dahulu demi meningkatkan kemungkinan mereka untuk menang. Dengan ilmu probabilitas ini, kita dapat memprediksi suatu kejadian berdasarkan sekumpulan data yang telah diolah dengan ilmu statistika. Inilah yang menyebabkan bahwa sebenarnya ilmu probabilitas dan statistika sangat dekat satu sama lain. [8]  

Kunci aplikasi probabilitas dalam statistik adalah memperkirakan terjadinya peluang atau probabilitas yang dihubungkan dengan terjadinya peristiwa tersebut dalam beberapa keadaan. Jika diketahui keseluruhan probabilitas dari kemungkinan outcome yang terjadi, seluruh probabilitas kejadian tersebut akan membentuk suatu distribusi probabilitas. [1] Dari sekian banyak distribusi probabilitas, distribusi normal merupakan distribusi yang secara luas banyak digunakan dalam berbagai penerapan. Praktisnya, distribusi ini sangat berguna karena mampu memperlihatkan distribusi dari pengamatan acak pada banyak eksperimen, dan juga mampu memperlihatkan distribusi yang diperoleh saat kita mencoba memperkirakan parameter-parameter dari distribusi probabilitas yang lain. [5] 

Ada dua peran penting dari distribusi normal. Pertama, distribusi normal memiliki beberapa sifat yang mungkin untuk digunakan sebagai patokan dalam mengambil suatu kesimpulan berdasarkan hasil sampel yang diperoleh. Pengukuran sampel digunakan untuk menafsirkan parameter populasi. Kedua, distribusi normal sangat sesuai dengan distribusi empiris, sehingga dapat dikatakan bahwa semua kejadian alami akan membentuk distibusi ini. Karena alasan inilah sehingga distribusi ini dikenal sebagai distribusi normal dan grafiknya dikenal sebagai kurva normal atau kurva gauss. Karena begitu pentingnya ketepatan dalam pengambilan kesimpulan suatu pengukuran atau percobaan. [3] Oleh sebab itu, penulis tertarik untuk mengambil judul “Distribusi Normal” yang akan membahas lebih dalam mengenai distribusi normal.

 

1.2 Rumusan Masalah

Adapun rumusan masalah dalam paper ini adalah sebagai berikut :

a. Apa yang dimaksud dengan distribusi normal?

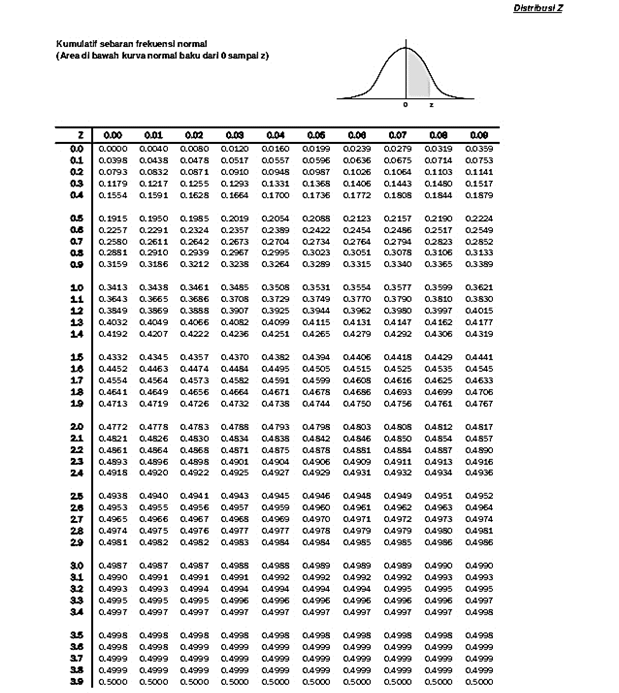
b. Bagaimana cara membaca tabel distribusi normal?

1.3 Tujuan

Berdasarkan latar belakang dan rumusan masalah diatas, Adapun tujuan dari paper ini adalah sebagai berikut :

a. Mengetahui dan memahami distribusi normal.

b. Mengetahui dan memahami cara membaca tabel distribusi normal.

Baca Juga : Distribusi Peluang Gabungan

BAB II

PEMBAHASAN

2.1 Distribusi Normal

    Distribusi normal merupakan suatu alat statistik yang sangat penting untuk menaksirkan dan meramalkan peristiwa – peristiwa yang lebih luas. Dikenalnya distribusi normal diawali oleh kemajuan yang pesat dalam pengukuran pada abad ke 19. Pada waktu itu, para ahli matematika dihadapkan pada suatu tantangan mengenai fenomena variabilitas pengamat atau interna yang artinya bila seorang mengadakan pengukuran berulang – ulang maka hasilnya akan berbeda – beda. Yang menjadi permasalahan adalah nilai manakah yang dianggap paling tepat dari semua hasil pengukuran tersebut. Berdasarkan kesepakatan maka nilai rata – rata dianggap paling tepat dan semua penyimpangan dari rata – rata dianggap suatu kesalahan atau error. [3] 

    Abraham de Moivre adalah yang pertama kali memperkenalkan distribusi normal ini dan kemudian dipopulerkan oleh Carl Fredreich Gauss. Sehingga nama lain distribusi ini adalah distribusi Gauss. Gauss mengamati hasil dari percobaan yang dilakukan berulang – ulang, dan menemukan hasil yang paling sering adalah nilai rata – rata. Penyimpangan baik ke kanan atau ke kiri yang jauh dari rata – rata, terjadinya semakin sedikit. Sehinggga bila disusun maka akan terbentuk distribusi yang simetris. Satu – satunya distribusi probabilitas dengan variabel random kontinu adalah distribusi normal. [3]

2.1.1 Kurva Normal

    Distribusi ini dijuluki kurva lonceng (bell curve) karena grafik fungsi kepekatan probabilitasnya mirip dengan bentuk lonceng seperti yang ditunjukkan pada gambar 2.1 berikut ini. [9]

           Gambar 2.1 Kurva Normal [3]

Suatu variabel acak kontinu X, yang memiliki distribusi disebut variabel acak normal. Persamaan matematika bagi distribusi probabilitas acak normal tergantung pada dua parameter, yaitu µ dan σ atau nilai tengah dan simpangan bakunya. Fungsi kepadatan probabilitas normal dapat dituliskan sebagai berikut. [7]

       Di mana : π = 3,14159

                           σ = simpangan baku = 

                           µ = rata – rata X

                        e  = 2,71828

Dalam gambar 2.2 diberikan sketsa dua kurva normal yang sama bentuknya, tetapi berpusat pada posisi yang berbeda sepanjang sumbu mendatar. 

Gambar 2.2 Kurva Normal dengan µ₁ ≠ µ_2, tetapi σ₁ = σ₂ [2]

Dalam gambar 2.3 diberikan sketsa dua kurva normal yang berpusat diposisi yang sama, tetapi kurva dengan simpangan baku yang lebih besar berbentuk lebih rendah dan lebih menyebar ke samping. 

Gambar 2.3 Kurva Normal dengan µ₁ = µ_2, tetapi σ₁ ≠ σ₂ [2]

Dalam gambar 2.4 menunjukkan sketsa dua kurva normal yang berpusat pada dua posisi yang berbeda, dan bentuk yang mencerminkan nilai σ yang berbeda juga.

Gambar 2.4 Kurva Normal dengan µ₁ ≠ µ_2, tetapi σ₁ ≠ σ₂ [2] 

Beberapa karakteristik distribusi normal adalah sebagai berikut. [7]

1.    Distribusi normal memiliki dua parameter yaitu µ dan σ yang masing – masing menentukan lokasi dan bentuk distribusi.

2.     Titik tertinggi kurva normal berada pada rata – rata.

3.     Distribusi normal adalah distribusi yang simetris.

4.   Simpangan baku (standar deviasi) σ, menentukan lebarnya kurva. Makin kecil σ bentuk kurva makin runcing.

5.  Total luas daerah di bawah kurva normal adalah 1. (Hal ini berlaku untuk seluruh distribusi probabilitas kontinu).

6.    Jika jarak dari masing – masing nilai X terhadap rata – rata µ diukur dengan simpangan baku σ, maka kira – kira 68% berjarak 1σ, 95% berjarak 2σ, dan 99% berjarak 3σ, atau ditulis sebagai berikut : 

P(µ - 1σ ≤ X ≤ µ + 1σ) = ± 68% (68,26%)

P(µ - 2σ ≤ X ≤ µ + 2σ) = ± 95% (95,46%)

P(µ - 3σ ≤ X ≤ µ + 3σ) = ± 99% (99,74%)

Untuk lebih jelasnya, dapat dilihat pada gambar 2.5 berikut ini.

Gambar 2.5 Kurva Normal dengan Skala Biasa (X) dan Skala Baru (Z) [6]

2.1.2 Distribusi Normal Baku (Standar)

Untuk mengubah distribusi normal menjadi distribusi normal baku (standar) sehingga diperoleh variabel baru Z adalah dengan menggunakan rumus sebagai berikut. [7]

Bila x berada diantara x = x₁ dan x = x_2, maka variabel acak z akan berada di antara nilai – nilai x tersebut. [7]

Perhatikan gambar 2.6 berikut ini.

Gambar 2.6 Populasi Normal Asal dan Hasil Transformasi

Dari gambar 2.6 diatas menunjukkan bahwa luas daerah antara x1 dan x2 sama dengan luas daerah z1 dan z2.

2.2 Cara Membaca Tabel Distribusi Normal

Perhatikan pada gambar 2.7 berikut ini.

Luas kurva normal disamakan dengan 1 satuan (100%), jadi kurva berbentuk simetris. Sehingga luas kurva sebelah kiri dan sebelah kanan titik O adalah 

Untuk mencari berapakah luas A pada gambar 2.7 diatas atau dapat digunakan tabel Distribusi Normal dengan melakukan cara berikut ini. [7]

1. Perhatikan harga tertinggi yang membatasi luas tersebut, dalam hal ini adalah 1,96, dan 

    uraikan menjadi 1,90 + 0,06.

2. Lihat kolom Z pada tabel distribusi normal dan cari di mana letak 1,90.

3. Setelah menemukan letak 1,90 segeralah bergeser ke arah kanan dan perhatikan 

   perpotongannya dengan kolom 0,06 (perpotongan baris 1,9 dengan kolom 0,06).

4. Pada perpotongan tersebut didapatkan angka sebesar 0,4750 yang merupakan luas A atau

 

Untuk lebih jelasnya, dapat dilihat pada gambar 2.8 berikut ini. 

BAB III

PENUTUP

3.1 Kesimpulan

Berdasarkan pembahasan yang telah penulis uraikan diatas, dapat disimpulkan bahwa:

1. Distribusi normal banyak digunakan dalam berbagai penerapan karena mampu memperlihatkan distribusi dari pengamatan acak pada banyak eksperimen. 

2.   Distribusi normal merupakan suatu alat statistik yang sangat penting untuk menaksirkan dan meramalkan peristiwa – peristiwa yang lebih luas.

3.    Distribusi normal pertama kali diperkenalkan oleh Abraham de Moivre dan dipopulerkan oleh Carl Fredreich Gauss.

4.  Distribusi normal dijuluki kurva lonceng (bell curve) karena grafik fungsi kepekatan probabilitasnya mirip dengan bentuk lonceng.

5.  Persamaan matematika bagi distribusi probabilitas acak normal tergantung pada dua parameter, yaitu nilai tengah (µ) dan simpangan bakunya (σ) yang masing – masing untuk menentukan lokasi dan bentuk distribusi.

6.   Dua kurva normal terdiri dari 3 kondisi yaitu, nilai tengah tidak sama tetapi simpangan baku sama, nilai tengah sama tetapi simpangan baku tidak sama, dan nilai tengah dan simpangan baku tidak sama.

7.   Karakteristik distribusi normal yaitu titik tertinggi kurva normal berada pada rata – rata, merupakan distribusi yang simetris, dan total luas daerah dibawah kurva normal adalah 1.

8.  Distribusi normal baku adalah distribusi normal yang memiliki rata-rata nol dan simpangan baku satu. 

3.2 Saran

Penulis menyadari bahwa dalam penulisan paper ini masih banyak kekurangan, oleh karena itu penulis mengharapkan kritik dan saran yang membangun dari pembaca agar penulisan paper ini kedepannya jauh lebih baik dari sebelumnya. Semoga paper ini bermanfaat bagi pembaca dan dapat menambah pustaka keilmuan mahasiswa.

DAFTAR PUSTAKA

[1]      Endista, Amiyella. Tanpa Tahun. "Distribusi Probabilitas". https://www.academia.edu/30148253/Distribusi_probabilitas, diakses 6 November 2020 pukul 18.50.

[2]      Harlyan, Ledhyane Ika. 2012. "Ukuran Pemusatan, Penyebaran dan Pola Distribusi Normal". http://ledhyane.lecture.ub.ac.id/files/2012/09/Ukuran-pemusatan-penyebaran-distribusi-normal1.pdf, diakses 20 November 2020 pukul 00.17.

[3]      Kaharuddin, Andi. 2018. "Distribusi Normal". https://www.researchgate.net/publication/327645406_DISTRIBUSI_NORMAL, diakses 6 November 2020 pukul 21.36.

[4]      Pradana, Bintang Adtya. Tanpa Tahun. "Makalah Probabilitas". http://adtyadjavanet.blogspot.com/2013/11/makalah-probabilitas.html#, diakses 6 November 2020 pukul 23.20.

[5]      Rosdianto, Haris., dan Moh. Toifur. 2017. "Implementasi Teori Distribusi Probabilitas Gaussian Pada Kualitas Rangkaian Penyearah Gelombang Penuh". Fisika dan Aplikasinya, 2(1). https://www.researchgate.net/publication/316596344_Implementasi_Teori_Distribusi_Probabilitas_Gaussian_Pada_Kualitas_Rangkaian_Penyearah_Gelombang_Penuh, diakses 20 November 2020 pukul 21.28.

[6]      Sulaiman, Susan. Tanpa Tahun. "Variabel Acak dan Distribusi Probabilitas Kontinu". PDF File.

[7]      Supranto, J. 2009. " Edisi Ketujuh Statistik Teori dan Aplikasi". Jakarta: Erlangga.

[8]      Totok, Made Gde Aghes Saktiasher. 2010. "Aplikasi Probabilitas dan Statistika Dalam Bidang Sistem Informasi Manajemen". https://informatika.stei.itb.ac.id/~rinaldi.munir/Probstat/2010-2011/Makalah2010/MakalahProbstat2010-020.pdf, diakses 5 November 2020 pukul 23.18.

[9]      Universitas Sumatera Utara. Tanpa Tahun. "Kajian Tentang Pendekatan Distribusi Binomial Oleh Distribusi Normal". http://repository.usu.ac.id/bitstream/handle/123456789/34193/Chapter%20I.pdf?sequence=4&isAllowed=y, diakses 6 November 2020 pukul 23.58. 

[10]    Zakaria. Tanpa Tahun. "Tabel t, z dan f dan chi kuadrat". https://www.slideshare.net/cvrhmat/tabel-t-z-dan-f-dan-chi-kuadrat-15912818, diakses 20 November 2020 pukul 20.22.

LAMPIRAN

TABEL DAERAH DISTRIBUSI NORMAL STANDAR [10]