Bilangan Kompleks I : Sifat Operasi Bilangan kompleks - Materi, Contoh Soal dan Latihan Soal
Pada blog kali ini akan membahas mengenai bilangan kompleks. Bilangan kompleks ini sering dipakai di bidang teknik elektro yang salah satunya digunakan untuk menggambarkan sifat arus AC (listrik arus bolak - balik), sehingga penting sekali buat kalian yang mengambil jurusan teknik elektro untuk mempelajari bilangan kompleks ini.
Untuk mengetahui lebih lanjut mengenai bilangan kompleks, mari kita masuk ke materi pembahasannya.
A. PENGANTAR
1. SIFAT OPERASI BILANGAN KOMPLEKS
b. Pengurangan
Pengurangan dua buah bilangan kompleks yaitu Z1 Z dinyatakan sebagai :
Perkalian dua buah bilangan kompleks yaitu Z1 Z dinyatakan sebagai :
Dalam matematika, bilangan kompleks adalah bilangan yang berbentuk
a + ib
dimana a,b adalah bilangan riil
i adalah bilangan imajiner
Namun sebelum itu, apakah kalian tahu apa itu bilangan riil dan bilangan imajiner? Bagi kalian yang masih belum mengetahui ataupun ingin sekedar mengingat kembali bilangan tersebut, berikut penjelasannya dibawah ini.
Dalam dunia matematika pastinya sudah tidak asing yang namanya bilangan bulat. Seperti yang kita ketahui bahwa bilangan bulat merupakan bilangan yang terdiri dari bilangan cacah yaitu 0,1,2,3,4,dst, dan bilangan negatif yaitu -1,-2,-3,-4,dst.
Dalam bilangan bulat, bila menghasilkan suatu pecahan maka disebut dengan bilangan rasional. Bilangan rasional merupakan suatu bilangan yang dapat dinyatakan sebagai bentuk a/b (pecahan) dimana a dan b adalah bilangan bulat dengan b bukan nol [2]. contoh bilangan rasional adalah sebagai berikut.
Gambar 2. Contoh bilangan rasional [4]
Kebalikan dari bilangan rasional dinamakan bilangan irasional. Bilangan irasional terdiri dari kumpulan bilangan yang tidak dapat dinyatakan dalam bentuk pecahan. Contoh yang paling populer dari bilangan irasional adalah sebagai berikut.
Gambar 3. Contoh bilangan irasional
Bilangan yang terdiri dari bilangan rasional dan bilangan irasional disebut dengan bilangan riil. Bilangan riil merupakan suatu bilangan yang dapat dibentuk menjadi desimal, sehingga bilangan riil ini meliputi bilangan rasional dan irasional yang direpresentasikan dalam bentuk desimal, contohnya seperti 3,51.
Bilangan imajiner atau biasa disebut bilangan khayal merupakan bilangan yang mempunyai sifat
Gambar 4. Sifat bilangan imajiner
Secara definisi, bilangan imajiner ini diperoleh dari penyelesaian persamaan kuadratik [3] :
atau secara ekuivalen
atau juga sering dituliskan sebagai
Karena itu terciptalah bilangan imajiner yang lebih populer disimbolkan dengan i (atau j dalam bidang kelistrikan), yang secara matematis memiliki kuantitas yang bersesuaian dengan akar dua dari negatif satu. sehingga untuk mendapatkan solusi terhadap persamaan diatas dapat memulainya dengan suatu anggapan i sebagai akar dua dari negatif satu [6].
Berikut contoh lain untuk bilangan imajiner.
Kesimpulan dari bilangan imajiner ini adalah bila menemukan bilangan negatif yang diakarkuadratkan atau bentuk akar negatif, maka itu merupakan bilangan imajiner yang dapat dinotasikan sebagai i.
Mari kita kembali ke bilangan kompleks pada bagian pembahasan berikut.
atau secara ekuivalen
atau juga sering dituliskan sebagai
Karena itu terciptalah bilangan imajiner yang lebih populer disimbolkan dengan i (atau j dalam bidang kelistrikan), yang secara matematis memiliki kuantitas yang bersesuaian dengan akar dua dari negatif satu. sehingga untuk mendapatkan solusi terhadap persamaan diatas dapat memulainya dengan suatu anggapan i sebagai akar dua dari negatif satu [6].
Berikut contoh lain untuk bilangan imajiner.
Gambar 5. Contoh bilangan imajiner
Mari kita kembali ke bilangan kompleks pada bagian pembahasan berikut.
B. PEMBAHASAN
Sebelum kita lanjut lebih jauh, berikut contoh bilangan kompleks.
Gambar 6. Contoh bilangan kompleks
1. SIFAT OPERASI BILANGAN KOMPLEKS
Seperti pada bilangan - bilangan lainnya, bilangan kompleks juga memiliki sifat - sifat operasi. Berikut sifat operasi tersebut.
a. Penjumlahan
Penjumlahan dua buah bilangan kompleks yaitu Z1 Z dinyatakan sebagai :
a. Penjumlahan
Penjumlahan dua buah bilangan kompleks yaitu Z1 Z dinyatakan sebagai :
Z1 = (a + ib)
Z2 = (c + id)
Z1 + Z2 = (a + ib) + (c + id) = (a + c) + (b + d)i
b. Pengurangan
Pengurangan dua buah bilangan kompleks yaitu Z1 Z dinyatakan sebagai :
Z1 = (a + ib)
Z2 = (c + id)
Z1 - Z2 = (a + ib) - (c + id) = (a - c) + (b - d)i
c. Perkalian
Perkalian dua buah bilangan kompleks yaitu Z1 Z dinyatakan sebagai :
Z1 = (a + ib)
Z2 = (c + id)
Z1 . Z2 = (a + ib) (c + id) = (ac - bd) + (ad + cb)i
Rumus tersebut didapat dari

d. Pembagian
Pembagian dua buah bilangan kompleks yaitu Z1 Z dinyatakan sebagai :
Z1 = (a + ib)
Z2 = (c + id)
Rumus tersebut didapat dari


2. BENTUK INVERS BILANGAN KOMPLEKS
Bentuk invers atau kebalikan dari suatu bilangan kompleks adalah sebagai berikut.
Rumus tersebut didapat dari


CONTOH SOAL BILANGAN KOMPLEKS
Berikut ini contoh soal bilangan kompleks berdasarkan materi yang sudah kita pelajari diatas.
Jika Z1 = 8 + 10i dan Z2 = 3 + 9i, maka hitung:
a. Z1 - Z2
b. Z1 . Z2
c. 2 Z2 - 2 Z1
b. Invers dari Z2
JAWAB
a. Z1 - Z2 = (8 + 10i) - (3 + 9i)
= - 3 + 8 - 9i + 10i
= 5 + i
b. Z1 . Z2 = (8 + 10i) (3 + 9i)
= 24 + 72i + 30i + 90i2
= 24 + 102i + 90(-1)
= - 66 + 102i
c. 2 Z2 - 2 Z1 = 2(3 + 9i) - 2(8 + 10i)
= 6 + 18i - 16 - 20i
= 6 - 16 + 18i - 20i
= - 10 - 2i
d. Invers dari Z2
LATIHAN SOAL BILANGAN KOMPLEKS
Setelah mempelajari contoh soal diatas, waktunya menguji kalian dengan mengerjakan latihan soal berikut ini. Selamat mengerjakan!
(1) Jika Z1 = 6 - 8i dan Z2 = - 9 - 3i, maka hitung:
a. Z1 . Z2
b. Z1 + 3 Z2 - 2
c. Z2 (1/2 Z1)
d. Z1-1+ Z2-1
(3) Sederhanakanlah
(4) Jika Z1 = 2 + 5i dan Z2 = - 3 - i, maka hitung:
Jika sudah mencoba mengerjakan latihan soal diatas, kalian bisa cek hasil jawabannya di video berikut ini.
Setelah kalian mempelajari beberapa materi mengenai bilangan kompleks hingga mengerjakan latihan soal diatas, semoga kalian dapat memahami dan lancar dalam mengerjakan bilangan kompleks. Jika kalian masih merasa bingung mengenai materi hingga latihan soal diatas kalian bisa comment dibawah untuk bertanya.
Untuk post bilangan kompleks bagian 1 saya akhiri sampai disini. Silahkan klik link berikut ini untuk mendapatkan materi bilangan kompleks lainnya.
Bilangan Kompleks II : Bentuk Kartesian Bilangan Kompleks
Untuk mengetahui aplikasi dari bilangan kompleks, bisa dibaca : Variabel Kompleks : Aplikasi Bilangan Kompleks - Analisis Sinyal [PAPER]
Jika post ini bermanfaat, jangan lupa share ke teman - teman kalian ya!
Thank you and see you in the next post! :)
Sumber :
[2]https://dsmlmdblog.blogspot.com/2015/02/bilangan-imajiner.html
[3]https://matematiku.wordpress.com/2010/01/21/bilangan-imajiner-sejarah-dan-filosofinya/
[4]https://satriaskyterror.wordpress.com/2012/02/05/sifat-bilangan-kompleks/
[5]https://www.pinterpandai.com/bilangan-kompleks/
[6]https://www.slideshare.net/ridhomjpolman/bab-5-bilangan-kompleks-70586091?qid=c995a982-fbc4-4cc2-8f33-111054284b29&v=&b=&from_search=4
[7]https://www.slideshare.net/bagustris/bab2-66360693?qid=7462e3ef-d798-4b4c-832c-584ded7c6933&v=&b=&from_search=1
[8]https://www.academia.edu/7118645/BILANGAN_KOMPLEKS_BILANGAN_KOMPLEKS_BILANGAN_KOMPLEKS_BILANGAN_KOMPLEKS
[3]https://matematiku.wordpress.com/2010/01/21/bilangan-imajiner-sejarah-dan-filosofinya/
[4]https://satriaskyterror.wordpress.com/2012/02/05/sifat-bilangan-kompleks/
[5]https://www.pinterpandai.com/bilangan-kompleks/
[6]https://www.slideshare.net/ridhomjpolman/bab-5-bilangan-kompleks-70586091?qid=c995a982-fbc4-4cc2-8f33-111054284b29&v=&b=&from_search=4
[7]https://www.slideshare.net/bagustris/bab2-66360693?qid=7462e3ef-d798-4b4c-832c-584ded7c6933&v=&b=&from_search=1
[8]https://www.academia.edu/7118645/BILANGAN_KOMPLEKS_BILANGAN_KOMPLEKS_BILANGAN_KOMPLEKS_BILANGAN_KOMPLEKS

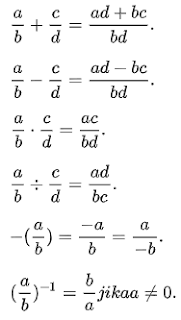














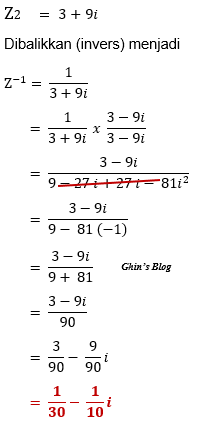





Barakallah Fii Ilmi authorr, semoga bisa bermanfaat untuk orang banyak 😊😊
ReplyDeleteWafiika barakallah, Aamiin. Terima kasih :)
Delete