Bilangan Kompleks II : Bentuk Kartesian Bilangan Kompleks - Materi, Contoh Soal, dan Latihan Soal

-

Hello readers!!

Pada post kali ini, ghin's blog akan melanjutkan bahasan sebelumnya yaitu mengenai bilangan kompleks. Bagi kalian yang belum baca post sebelumnya, kalian bisa buka link berikut ini.


Langsung saja kita lanjut bahasan bilangan kompleks bagian 2, Selamat membaca!

3. BENTUK PENYAJIAN BILANGAN KOMPLEKS

Terdapat beberapa bentuk penulisan atau penyajian bilangan kompleks, di antaranya yaitu :
    a. Bentuk Rectangular (Kartesian)
    b. Bentuk Polar
    c. Bentuk Eksponensial

a. Bentuk Rectangular (Kartesian)   

Bilangan kompleks bentuk kartesian dinyatakan dalam bentuk z = x + iy atau z = a + ib
x, y, a, b = bilangan nyata/real
i             = bilangan khayal (imajiner)
x, a        = bilangan real dari z, Re(z)
y, b        = bilangan imajiner dari z, Im(z)

Bilangan kompleks adalah pasangan terurut dari dua bilangan real x dan y, yang dinyatakan oleh (x,y) [1].

Bilangan kompleks memiliki dua komponen yaitu bagian nyata/real dan imajiner. Penggambaran bilangan kompleks juga disebut bidang kompleks atau bidang z yang digunakan berdasarkan pada sistem koordinat kartesian. Bilangan kompleks z = x + iy yang bersesuaian dengan titik P(x,y) menunjukkan bahwa koordinat kartesian pada sumbu x berisi semua bilangan nyata/real yang disebut sumbu nyata/real, dan sumbu y berisi semua bilangan kompleks yang murni imajiner (yaitu tidak memiliki bagian nyata), dan disebut sebagai sumbu imajiner.
Gambar 1. Koordinat Kartesian Bilangan Kompleks
Selain bidang kompleks atau bidang z, penggambaran bilangan kompleks juga disebut bidang argand. Diagram yang mewakili bilangan kompleks di bidang argand disebut diagram argand [8], yang dinamai dari ahli matematika Swiss Jean Argand (1768-1822) [6].  
Gambar 2. Bidang Kompleks
Operasi penjumlahan dan operasi pengurangan dari dua bilangan kompleks dapat dilihat menggunakan bidang kompleks, seperti yang terlihat pada gambar 3 dan gambar 4 berikut ini.
                     
                                                Gambar 3. Penjumlahan Dua Bilangan Kompleks
  
Gambar 4. Pengurangan Dua Bilangan Kompleks 
          








2. KONJUGAT KOMPLEKS

Konjugat kompleks  atau z* dari bilangan kompleks z = x +iy didefinisikan sebagai 

 = x - iy
 
Konjugat kompleks diperoleh dengan mengalikan bagian imajiner (i) dengan -1.

Pada gambar 5 dibawah ini menggambarkan bilangan konjugat kompleks yang diperoleh dari pencerminan titik z terhadap sumbu x (sumbu nyata/real) pada garis horizontal.
Gambar 5. Konjugat Kompleks
Sifat - sifat konjugat kompleks dapat dilihat sebagai berikut.

3. MODULUS BILANGAN KOMPLEKS

Seperti yang kita sudah ketahui bahwa bilangan kompleks z = a + ib dapat digambarkan dalam bentuk bidang kompleks seperti pada gambar 2. Bagaimana kita dapat menemukan jarak titik dari asalnya atau panjang OP yang dapat dilihat pada gambar 2 tersebut? Dari gambar 2 kita buat seperti pada gambar 6 berikut ini.
Gambar 6. Bidang Kompleks Untuk Menentukan Panjang OP
Berdasarkan pada gambar 6 diatas dapat diketahui bahwa OM = a dan ON = MP = b. Maka, panjang OP dapat diketahui dengan menggunakan phytagoras. 


Panjang OP itulah yang disebut dengan modulus atau nilai absolut dari bilangan kompleks a+ib [8].

Modulus dari bilangan kompleks z = x + iy didefinisikan sebagai jarak antara z dengan pusat sumbu dan dituliskan 
|z| = |x + iy| = 

yang dinyatakan sebagai panjang vektor z, yaitu jarak dari titik O = (0,0) terhadap titik z = (x,y), seperti pada gambar 7 dibawah ini.
Gambar 7. Modulus Pada Bilangan Kompleks
Jika z1 = x1 + iy1 dan z2 = x2 + iy2, maka 
|z1 - z2| = 

yang dinyatakan sebagai jarak antara titik z1 dan z2 pada bidang z, seperti pada gambar 8 dibawah ini.
Gambar 8. Modulus Pada Dua Bilangan Kompleks

Sifat - sifat modulus bilangan kompleks dapat dilihat sebagai berikut.
         
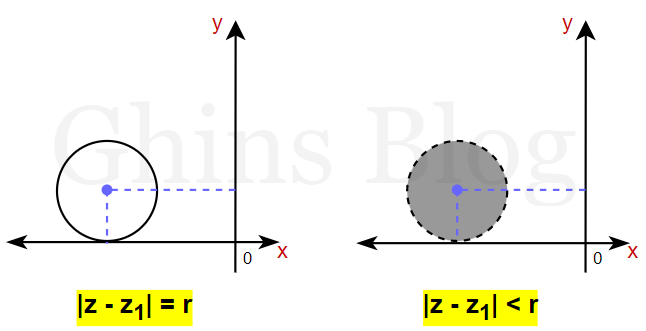
Jika z1 = x1 + iy1 dan r adalah bilangan real positif, maka
    |z - z1| = r ; lingkaran berpusat di titik z1 = (x1,y1) berjari - jari r
    |z - z1| < r ; daerah di dalam lingkaran yang berpusat di titik z1 = (x1,y1) berjari - 
                       jari r
                  

                CONTOH SOAL BILANGAN KOMPLEKS

Berikut ini contoh soal bilangan kompleks berdasarkan materi yang sudah kita pelajari diatas.

Jika z1  = 5 + 2i dan z2 =  1 + 6i
a. Gambarkan bilangan kompleks z1 + z2 dan 
b. Hitunglah  
c. Gambarkan |z + z2| = 2
d. Gambarkan |z - z2| < 2

JAWAB



a. z1 + z2 = (5+2i) + (1+6i)
               = (5+1) + (2+6)i
               = 6+8i 

    = (5-2i) + (1-6i)
                  = (5+1) + (-2-6)i
                  = 6-8i
        
b.  = |(8-10i)(3-9i) - (8+10i)(3+9i)|
                           = |(24-72i-30i+(90.(-1))) - (24+72i+30i+(90.(-1)))
                           = |(24-102i-90) - (24+102i-90)|
                           = |(-66-102i) - (-66 +102i)|
                           = |-102i-102i|
                           = |-204i|
                           = 
                           = 204

c. Misalkan z = x+iy                                                         
    |z + z2| = 2                                                       
    |x+iy+3+9i| = 2
    |(x+3)+(y+9)i| = 2
                                  
      
    Persamaan lingkaran yang berpusat di titik (-3,-9) berjari - jari 2
       

d. Misalkan z = x+iy                                                         
    |z + z2| < 2                                                       
    |x+iy+3+9i| < 2
    |(x+3)+(y+9)i| < 2
    
    
    Daerah di dalam lingkaran yang berpusat di titik (-3,-9) berjari - jari 2
    



LATIHAN SOAL BILANGAN KOMPLEKS

Setelah mempelajari contoh soal diatas, waktunya menguji kalian dengan mengerjakan latihan soal berikut ini. Selamat mengerjakan!

Jika z1  = 6 - 8i, z2 =  -9 - 3i, dan z3 = + 2i
a. Gambarkan bilangan kompleks z1 - z2, -z1 - z2,  
b. Hitunglah 
c. Hitunglah 

Gambarkan grafik 
a. |z - 3i| = 6
b. | (z - 4) / (z + 4) | < 3
c. |z + 3| = |z - 6| 

Jika sudah mencoba mengerjakan latihan soal diatas, kalian bisa cek hasil jawabannya di video berikut ini.



Setelah kalian mempelajari beberapa materi bilangan kompleks mengenai bentuk kartesian bilangan kompleks hingga latihan soal diatas, semoga kalian dapat memahami dan lancar dalam mengerjakan soal bilangan kompleks. Kalian bisa comment dibawah bila kalian mengalami kesulitan dalam memahami materi atau saat mengerjakan latihan soal diatas.

Untuk post bilangan kompleks bagian 2 saya akhiri sampai disini. Silahkan klik link berikut ini untuk mendapatkan materi bilangan kompleks lainnya.



Bilangan Kompleks III : Bentuk Polar dan Eksponensial

Untuk mengetahui aplikasi dari bilangan kompleks, bisa dibaca : Variabel Kompleks : Aplikasi Bilangan Kompleks - Analisis Sinyal [PAPER]

Jika post ini bermanfaat, jangan lupa share ke teman - teman kalian ya!

Thank you, and see you in the next post!

Sumber :

[1] http://repository.ut.ac.id/3865/1/MATA4322-M1.pdf
[2] https://www.slideshare.net/agus_budiarto/bilangan-kompleks-lengkap
[3] https://repository.unmul.ac.id/bitstream/handle/123456789/13562/Pertemuan%207_Bilangan%20Kompleks.pdf?sequence=1
[4] Ratnadewi. dkk. 2019. "MATEMATIKA TEKNIK". Bandung: Rekayasa Sains.
[5] https://teknik.uma.ac.id/wp-content/uploads/2019/07/46.pdf
[6] https://www.cimt.org.uk/projects/mepres/alevel/fpure_ch3.pdf
[7] https://www.maths.ox.ac.uk/system/files/attachments/complex_1.pdf
[8] https://nios.ac.in/media/documents/SrSec311NEW/311_Maths_Eng/311_Maths_Eng_Lesson8.pdf

Comments

Post a Comment

Popular posts from this blog

Deret Angka : Pengertian, Contoh Soal, dan Latihan Soal

-
Image
Hello readers!! Kali ini saya akan membahas mengenai DERET ANGKA yang biasanya muncul dalam soal psikotes. Namun sebelum itu, apakah kalian tahu apa itu psikotes? Psikotes adalah tes yang bertujuan untuk memberikan gambaran mengenai aspek - aspek psikis seseorang sesuai dengan kebutuhan dan keperluan klien (perusahaan atau instansi). Dalam psikotest terdiri dari berbagai jenis tes. Tes yang sering digunakan seperti tes kemampuan verbal, tes kemampuan numerik, tes kemampuan penalaran, tes kemampuan spasial, maupun tes kepribadian. [1] Dari berbagai jenis tes yang telah disebutkan diatas, deret angka termasuk ke dalam tes kemampuan numerik yang mana tujuan dari tes kemampuan numerik adalah untuk mengetahui kemampuan berhitung seseorang dengan cermat dan cepat dalam waktu yang terbatas. [1] Bagi kalian yang masih kurang memahami mengenai deret angka, di dalam blog ini akan saya bahas tuntas satu persatu secara detail dengan penuh contoh -  contoh soal sehingg...
Read more

Variabel Kompleks : Aplikasi Bilangan Kompleks - Analisis Sinyal [PAPER]

-
Image
  BAB I PENDAHULUAN 1.1 Latar Belakang Himpunan bilangan kompleks yang secara umum disimbolkan dengan C, telah banyak diaplikasikan di fisika. Munculnya konsep bilangan kompleks secara alamiah pada abad ke-16 yaitu ketika para matematikawan hendak mengekspresikan seluruh akar dari polynomial. Bilangan interger dapat menyelesaikan persamaan seperti: x + 1 = 0, dan bilangan rasional dapat menyelesaikan seperti: 2x - 1 = 0, serta bilangan nyata (real) dapat menyelesaikan persamaan seperti: x² + 1 = 0. Himpunan bilangan kompleks akhirnya dapat mengekspresikan seluruh akar dari setiap polynomial. [5] Salah satu aplikasi dari bilangan kompleks adalah analisis sinyal. Analisis dan prediksi performansi dari sistem telekomunikasi berdasarkan power atau daya yang didistribusikan dan analisis frekuensi dari sinyal yang di transmisikan dalam mendesain sebuah sistem telekomunikasi yang handal dapat dilakukan dengan analisis sinyal secara matematis. Secara teknik, sinyal adalah kuantitas fisik y...
Read more

Bilangan Kompleks I : Sifat Operasi Bilangan kompleks - Materi, Contoh Soal dan Latihan Soal

-
Image
Hello readers!! Pada blog kali ini akan membahas mengenai bilangan kompleks . Bilangan kompleks ini sering dipakai di bidang teknik elektro yang salah satunya digunakan untuk menggambarkan sifat arus AC (listrik arus bolak - balik), sehingga penting sekali buat kalian yang mengambil jurusan teknik elektro untuk mempelajari bilangan kompleks ini.  Untuk mengetahui lebih lanjut mengenai bilangan kompleks, mari kita masuk ke materi pembahasannya. A. PENGANTAR Dalam matematika, bilangan kompleks adalah bilangan yang berbentuk  a + ib dimana a,b adalah bilangan riil               i  adalah bilangan imajiner Namun sebelum itu, apakah kalian tahu apa itu bilangan riil dan bilangan imajiner? Bagi kalian yang masih belum mengetahui ataupun ingin sekedar mengingat kembali bilangan tersebut, berikut penjelasannya dibawah ini. Dalam dunia matematika pastinya sudah tidak asing yang namanya bilangan bulat. Seperti ya...
Read more